Cell Growth and Division
Each cell has three parameters associated with its growth: growth rate, growth axis, and anisotropy. The driving force for cell growth is turgor pressure. This causes the walls (springs) to be in tension and have an associated extension. In this state the cell cannot easily expand due to the stiffness of the springs forming its walls. By resetting the natural length of the cell’s springs, we can simulate structural changes in the cell wall that relieve the tension and allow further growth. In this way pressure drives expansion by stretching the walls and the cell responds by restructuring the walls to allow more extension.
Each cell has three parameters associated with its growth: growth rate, growth axis, and anisotropy. The driving force for cell growth is turgor pressure. This causes the walls (springs) to be in tension and have an associated extension. In this state the cell cannot easily expand due to the stiffness of the springs forming its walls. By resetting the natural length of the cell’s springs, we can simulate structural changes in the cell wall that relieve the tension and allow further growth. In this way pressure drives expansion by stretching the walls and the cell responds by restructuring the walls to allow more extension.

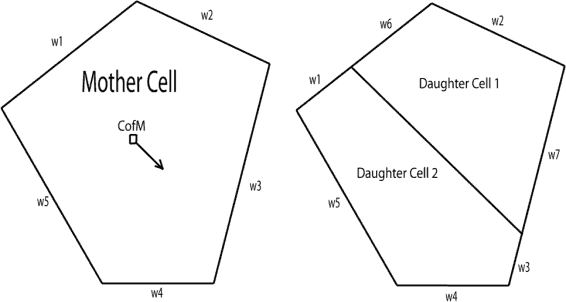
Cell division is instigated by the genetic script of the dividing cell. All divisions are currently approximately symmetric. The dividing wall is inserted parallel to the division orientation vector and passing through the centre of mass of the cell. Any existing walls forming the boundary of the dividing cell that are intersected by the dividing wall are split into two halves. The resulting set of walls is allocated to two new cells either side of the dividing wall as shown below:
Spatio-mechanical model for cell walls.
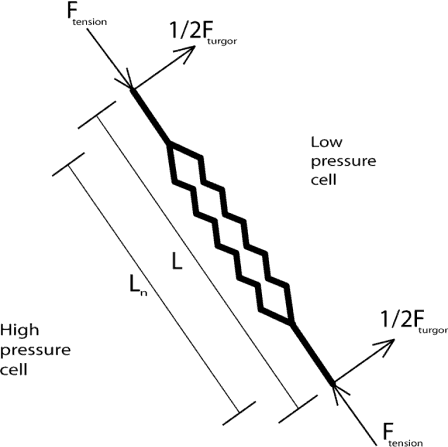
The spatial model is two-dimensional with cells restricted to a single plane. Each cell has a closed boundary described by a set of linear elements called walls. Each wall forms the interface between two cells or between a cell and the external environment. The geometry of the walls is described by a set of vertices, the points where walls intersect. The ultimate output of the spatial model is the positions of these vertices. Walls are modelled as a set of springs, one for each adjacent cell, attached to two vertices.
Each spring has fixed stiffness. The natural length of each spring is determined by the state parameters of the appropriate cell. Cell growth is achieved by increasing the natural length of the springs associated with the growing cell. Each cell also has a turgor pressure which exerts a force perpendicular to each wall in an outward direction with respect to the cell.
The spatial model is two-dimensional with cells restricted to a single plane. Each cell has a closed boundary described by a set of linear elements called walls. Each wall forms the interface between two cells or between a cell and the external environment. The geometry of the walls is described by a set of vertices, the points where walls intersect. The ultimate output of the spatial model is the positions of these vertices. Walls are modelled as a set of springs, one for each adjacent cell, attached to two vertices.
Each spring has fixed stiffness. The natural length of each spring is determined by the state parameters of the appropriate cell. Cell growth is achieved by increasing the natural length of the springs associated with the growing cell. Each cell also has a turgor pressure which exerts a force perpendicular to each wall in an outward direction with respect to the cell.